2458. Height of the Binary Tree

Height of Binary Tree After Subtree Removal Queries

Leetcode 2458.

Today in the daily Leetcode problem of the day, we have a hard-level question related to trees.

But first Let’s understand the question

We have a Binary Tree with n nodes with unique values from 1 to n.

We have given queries[i] of size n which are independent. We have to perform queries[i] such that we Remove the subtree rooted at the node with the value queries[i] from the tree. Remember, It is guaranteed that queries[i] will not be equal to the value of the root.

Constraints:

• The number of nodes in the tree is n.
• 2 <= n <= 105
• 1 <= Node.val <= n
• All the values in the tree are unique.
• m == queries.length
• 1 <= m <= min(n, 104)
• 1 <= queries[i] <= n
• queries[i] != root.val

Our task is to Return an array answer of size m where answer[i] is the height of the tree after performing the ith query.

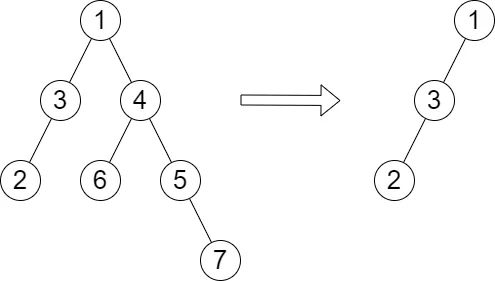
Input: root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4] Output: [2] Explanation: The diagram above shows the tree after removing the subtree rooted at node with value 4. The height of the tree is 2 (The path 1 -> 3 -> 2).

Let’s perform queries by taking an example:-

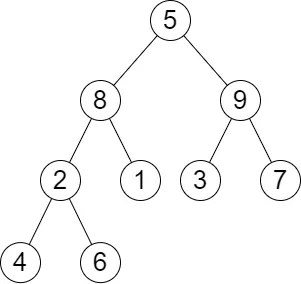
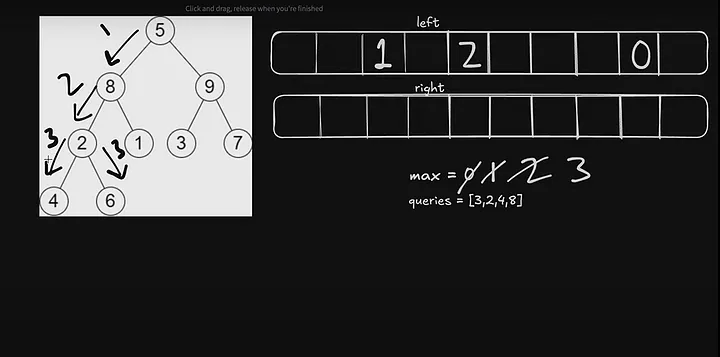
Input: root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8] Output: [3,2,3,2]

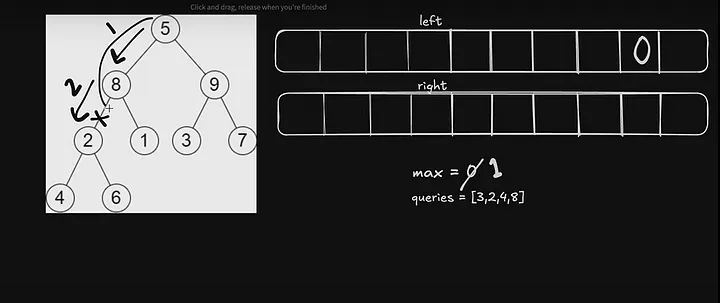
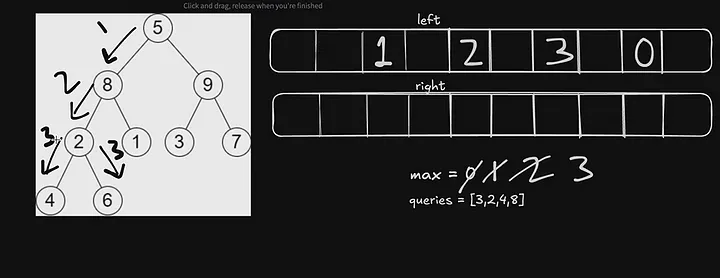
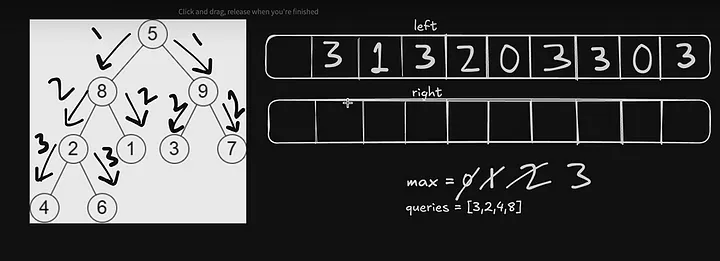
Basically, we have to see after removing the queries node our tree height is disturbing or not. For that, we will calculate the maximum depth of the tree from both the left and right sides of the tree.

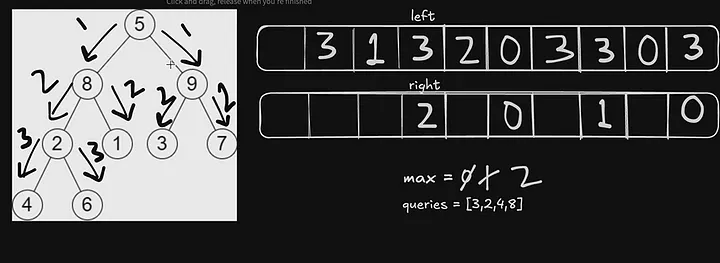
Now, Let’s see through right side

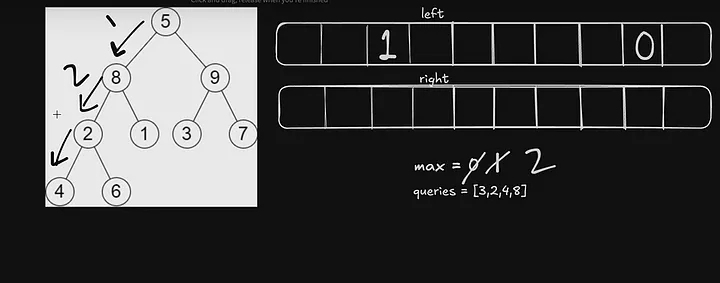
Now we will put index 6 as max 2. And if we include 6 the height max. would be 3

Now, We will perform DFS traversal on both sides of the tree to perform the queries[i] by Remove and check whether after removing the form left can get the maximum height from the right side or vice versa just as mentioned in the problem statement.

Now let’s write code in Java

class Solution {
    int max;
    public int[] treeQueries(TreeNode root, int[] queries) {
        int left[] = new int[100001];
        int right[] = new int[100001];   

        max = 0;
        leftFirst(root, left, 0);
        max = 0;
        rightFirst(root, right, 0);
        
        for(int i=0; i<queries.length; i++){
            queries[i] = Math.max(left[queries[i]], right[queries[i]]);
        }
        return queries;
    }

    private void leftFirst(TreeNode root, int[] left, int d) {
        if(root == null) return;
        left[root.val] = max;
        max = Math.max(max, d); // d = deapth
        leftFirst(root.left, left, d+1);
        leftFirst(root.right, left, d+1);
    }

    private void rightFirst(TreeNode root, int[] right, int d) {
        if(root == null) return;
        right[root.val] = max;
        max = Math.max(max, d); // d = deapth
        rightFirst(root.right, right, d+1);
        rightFirst(root.left, right, d+1);
    }
}

The Time and Space Complexity would be O(n).